Babenko–Beckner inequality
In mathematics, the Babenko–Beckner inequality (after K. Ivan Babenko and William E. Beckner) is a sharpened form of the Hausdorff–Young inequality having applications to uncertainty principles in the Fourier analysis of Lp spaces. The (q, p)-norm of the n-dimensional Fourier transform is defined to be[1]
In 1961, Babenko[2] found this norm for even integer values of q. Finally, in 1975, using Hermite functions as eigenfunctions of the Fourier transform, Beckner[3] proved that the value of this norm for all 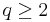 is
is
Thus we have the Babenko–Beckner inequality that
To write this out explicitly, (in the case of one dimension,) if the Fourier transform is normalized so that
then we have
or more simply
Contents |
Main ideas of proof
Throughout this sketch of a proof, let
(Except for q, we will more or less follow the notation of Beckner.)
The two-point lemma
Let 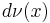 be the discrete measure with weight
be the discrete measure with weight 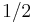 at the points
at the points 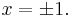 Then the operator
Then the operator
maps 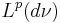 to
to 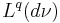 with norm 1; that is,
with norm 1; that is,
or more explicitly,
for any complex a, b. (See Beckner's paper for the proof of his "two-point lemma".)
A sequence of Bernoulli trials
The measure 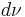 that was introduced above is actually a fair Bernoulli trial with mean 0 and variance 1. Consider the sum of a sequence of n such Bernoulli trials, independent and normalized so that the standard deviation remains 1. We obtain the measure
that was introduced above is actually a fair Bernoulli trial with mean 0 and variance 1. Consider the sum of a sequence of n such Bernoulli trials, independent and normalized so that the standard deviation remains 1. We obtain the measure 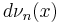 which is the n-fold convolution of
which is the n-fold convolution of 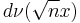 with itself. The next step is to extend the operator C defined on the two-point space above to an operator defined on the (n+1)-point space of
with itself. The next step is to extend the operator C defined on the two-point space above to an operator defined on the (n+1)-point space of 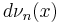 with respect to the elementary symmetric polynomials.
with respect to the elementary symmetric polynomials.
Convergence to standard normal distribution
The sequence 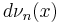 converges weakly to the standard normal probability distribution
converges weakly to the standard normal probability distribution 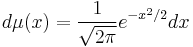 with respect to functions of polynomial growth. In the limit, the extension of the operator C above in terms of the elementary symmetric polynomials with respect to the measure
with respect to functions of polynomial growth. In the limit, the extension of the operator C above in terms of the elementary symmetric polynomials with respect to the measure 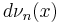 is expressed as an operator T in terms of the Hermite polynomials with respect to the standard normal distribution. These Hermite functions are the eigenfunctions of the Fourier transform, and the (q, p)-norm of the Fourier transform is obtained as a result after some renormalization.
is expressed as an operator T in terms of the Hermite polynomials with respect to the standard normal distribution. These Hermite functions are the eigenfunctions of the Fourier transform, and the (q, p)-norm of the Fourier transform is obtained as a result after some renormalization.
See also
References
- ^ Iwo Bialynicki-Birula. Formulation of the uncertainty relations in terms of the Renyi entropies. arXiv:quant-ph/0608116v2
- ^ K.I. Babenko. An ineqality in the theory of Fourier analysis. Izv. Akad. Nauk SSSR, Ser. Mat. 25 (1961) pp. 531-542 English transl., Amer. Math. Soc. Transl. (2) 44, pp. 115-128
- ^ W. Beckner, Inequalities in Fourier analysis. Annals of Mathematics, Vol. 102, No. 6 (1975) pp. 159–182.
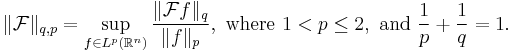
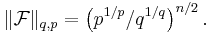
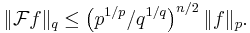
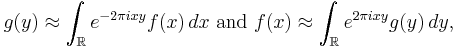
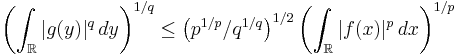
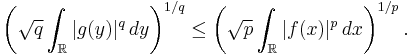
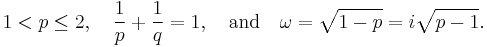
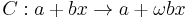
![\left[\int|a%2B\omega bx|^q d\nu(x)\right]^{1/q} \le \left[\int|a%2Bbx|^p d\nu(x)\right]^{1/p},](/2012-wikipedia_en_all_nopic_01_2012/I/59f21549a0364424388b4802769a019a.png)
![\left[\frac {|a%2B\omega b|^q %2B |a-\omega b|^q} 2 \right]^{1/q}
\le \left[\frac {|a%2Bb|^p %2B |a-b|^p} 2 \right]^{1/p}](/2012-wikipedia_en_all_nopic_01_2012/I/476b514cc4336161fccc5da99a6806c0.png)